Sample Spaces
Recall a probability experiment is an experiment with known outcomes. We named the collection of outcomes for a probability experiment:
Sample Space the collection of all possible outcomes of a probability experiment
Example: Consider the probability experiment of rolling a 6-sided dice. An example of an outcome is "rolling a 3". Often we will use set notation to indicate a sample space:
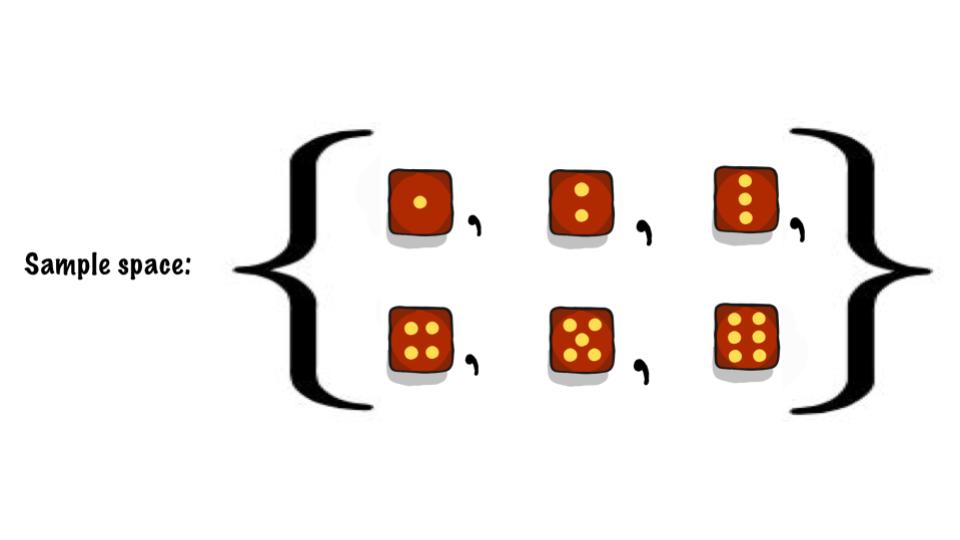
\[S=\{1,2,3,4,5,6\}\]
We will be attempting to find the probabilities (likely-hood) of certain events.
Event a sub-collection of outcomes of a probability experiment.
Example: Again for the example of rolling a 6-sided dice, and example of an event could be "rolling an even number"
.jpg)
\[E=\{2,4,6\}\]
To visualize (and eventually help count) the possible outcomes of an experiment we will use a tree diagram, or the "cross product".
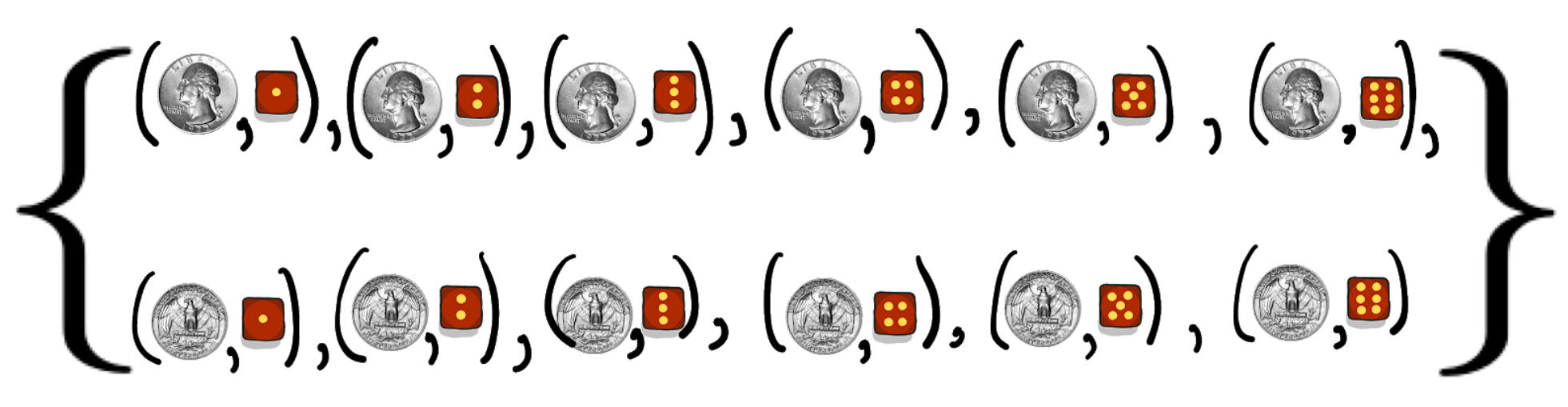
Example: Suppose the experiment is flipping a fair coin and then rolling a 6-sided die, then we can figure out all of the outcomes of the experiment with the following tree diagram
.jpg)
and we have the following set (cross-product) for our sample space: